Plot of the six trigonometric functions, the unit circle, and a line for the angle = radians The points labelled 1, Sec(θ), Csc(θ) represent the length of the line segment from the origin to that point Sin(θ), Tan(θ), and 1 are the heights to the line starting from the axis, while Cos(θ), 1, and Cot(θ) are lengths along the axis starting from the originFree trigonometric identities list trigonometric identities by request stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie Policy Learn more Accept Solutions Graphing Practice;Identities expressing trig functions in terms of their supplements Sum, difference, and double angle formulas for tangent The half angle formulas The ones for sine and cosine take the positive or negative square root depending on the quadrant of the angle θ/2 For example, if θ/2 is an acute angle, then the positive root would be used Truly obscure identities These are just here for
What Is The Formula Of Tan2x Quora
Tan^2x trig identity
Tan^2x trig identity-Now use the identity to replace sin 2 x and write the new integral Now this new integral is a sum of two integrals, the last of which can be evaluated easily using the substitution u = cos(x), like this The first integral is easy, it's just cos(x) The second is easy because of the substitution Now we just back substitute cos(x) for u to get the solution (don't forget the constant) WeAs there is no way to immediately integrate tan^2 (x) using well known trigonometric integrals and derivatives, it seems like a good idea would be writing tan^2 (x) as sec^2 (x) 1 Now, we can recognise sec^2 (x) as the derivative of tan (x) (you can prove this using the quotient rule and the identity sin^2 (x) cos^2 (x) = 1), while we get




How To Use Double Angle Identities Studypug
Tan(xy)= tan(x)tan(y) 1tan(x)tan(y) DIFFERENCE IDENTITIES sin(xy)=sin(x)cos(y)cos(x)sin(y) cos(xy) = cos(x)cos(y)sin(x)sin(y) tan(xy)= tan(x)tan(y) 1tan(x)tan(y) LAW OF SINES sin(A) a = sin(B) b = sin c DOUBLEANGLE IDENTITIES sin(2x)=2sin(x)cos(x) cos(2x) = cos2(x)sin2(x) = 2cos2(x)1 =12sin2(x) tan(2x)= 2tan(x) 1 2tan (x) HALFANGLETan(x y) = (tan x tan y) / (1 tan x tan y) sin(2x) = 2 sin x cos x cos(2x) = cos 2 (x) sin 2 (x) = 2 cos 2 (x) 1 = 1 2 sin 2 (x) tan(2x) = 2 tan(x) / (1Therefore in mathematics as well as in physics, such formulae are useful for deriving many important identities The trigonometric formulas like Sin2x, Cos 2x, Tan 2x are popular as double angle formulae, because they have double angles in their trigonometric functions For solving many problems we may use these widely The Sin 2x formula is \(Sin 2x = 2 sin x cos x\) Where x
In this video I go over the proof of the trigonometry identity tan^2(x) 1 = sec^2(x) The proof of this identity is very simple and like many other trig id Trig identity $1\tan x \tan 2x = \sec 2x$ 13 Which trigonometric identities involve trigonometric functions?Trig identities tan^2Trigonometric Identities Pythagoras's theorem sin2 cos2 = 1 (1) 1 cot2 = cosec2 (2) tan2 1 = sec2 (3) Note that (2) = (1)=sin 2 and (3) = (1)=cos CompoundThe half‐angle identity for tangent can be written in three different forms In the first form, the sign is determined by the quadrant in which the angle α/2 is located Example 5 Verify the identity Example 6 Verify
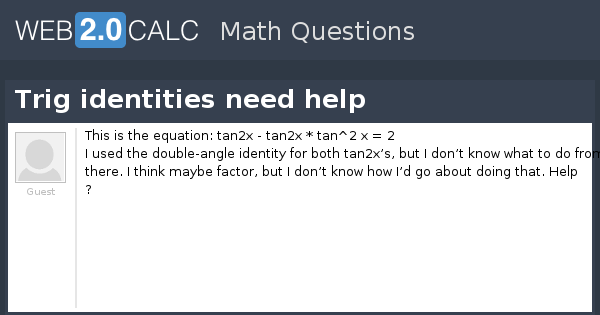
Here we will prove the problems on trigonometric identities As you know that the identity consists of two sides in equation, named Left Hand Side (abbreviated as LHS) and Right Hand Side (abbreviated as RHS)To prove the identity, sometimes we need to apply more fundamental identities, eg $\sin^2 x \cos^2 x = 1$ and use logical steps in order to lead oneTrig Identities Identities involving trig functions are listed below Pythagorean Identities sin 2 θ tan (x π) = tan x cot (x π) = cot x tan (x 180°) = tan x cot (x 180°) = cot x Sum/Difference Identities Double Angle Identities Half Angle Identities or or or or Product to Sum Identities Sum to Product Identities See also Sine, cosine, tangent, cosecantTrig identity $1\tan x \tan 2x = \sec 2x$ Ask Question Asked 10 years, 3 months ago Active 6 years, 1 month ago Viewed 6k times 3 0 $\begingroup$ I need to prove that $$1\tan x \tan 2x = \sec 2x$$ I started this by making sec 1/cos and using the double angle identity for that and it didn't work at all in any way ever Not sure why I can't do that, but something was wrong



1




Trig Identities Table Of Trigonometric Identities
Proving a trigonometric identity refers to showing that the identity is always true, no matter what value of x x x or θ \theta θ is used Because it has to hold true for all values of x x x, we cannot simply substitute in a few values of x x x to "show" that they are equal It is possible that both sides are equal at several values (namely when we solve the equation), and we might falsely2tan2 x = sec2 x for values of x in the interval 0 ≤ x < 2π We try to relate the given equation to one of our three identities We can use the identity sec2 x = 1tan2 x to rewrite the equation solely in terms of tanx 2tan2 x = sec2 x 2tan 2x = 1tan x from which tan2 x = 1 Taking the square root then gives tanx = 1 or − 1Definitions Trigonometric functions specify the relationships between side lengths and interior angles of a right triangle For example, the sine of angle θ is defined as being the length of the opposite side divided by the length of the hypotenuse The six trigonometric functions are defined for every real number, except, for some of them




Trigonometric Identities Simplify Expressions Video Lessons Examples And Solutions




Trig Identities Turn The Wheel
Account Details Login Options Account ManagementAccount Details Login Options Account Management True Start with the well known pythagorean identity sin^2x cos^2x = 1 This is readily derived directly from the definition of the basic trigonometric functions sin and cos and Pythagoras's Theorem Divide both side by cos^2x and we get sin^2x/cos^2x cos^2x/cos^2x = 1/cos^2x tan^2x 1 = sec^2x tan^2x = sec^2x 1 Confirming that the result is an identity




Solved 2 Prove The Following Trig Identities A Prove Tan Chegg Com




Integrate Sec 2x Method 2
Free trigonometric identity calculator verify trigonometric identities stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie Policy Learn more Accept Solutions Graphing Practice;Trig Identities STUDY Flashcards Learn Write Spell Test PLAY Match Gravity Created by connorbassett1 Terms in this set (32) Pythagorean Identity sin^2xcos^2x=1 Pythagorean Identity 1tan^2x=sec^2x Pythagorean Identity 1cot^2x=csc^2x Quotient Identity of Tangent tanθ = sinθ/cosθ Quotient Identity of Cotangent cotθ = cosθ/sinθ Reciprocal$\sec^2{x}\tan^2{x} \,=\, 1$ $\sec^2{A}\tan^2{A} \,=\, 1$ Remember, the angle of a right triangle can be represented by any symbol but the relationship between secant and tan functions must be written in that symbol Proof Learn how to prove the Pythagorean identity of secant and tan functions in mathematical form by geometrical method




Tan 2x Csc 2x Tan 2x 1 Problem Solving Solving Identity



Rlemke01 Math Tufts Edu
Power reducing Identity tan^2 x 1 cos (2x) / 1 cos (2x) half angle formula for sine sin (x/2) = / square root of ( 1cosx ) / 2 half angle formula for cosine cos (x/2) = / square root of ( 1 cosx ) / 2 half angle formula for tangent tan (x/2) = ( 1cosx ) / (sinx)This is probably the most important trig identity Identities expressing trig functions in terms of their complements There's not muchPDF Trigonometric identities are mathematical equations which are made up of functions These identities are true for any value of the variable put There are many identities which are derived by the basic functions, ie, sin, cos, tan, etc The most basic identity is the Pythagorean Identity, which is derived from the Pythagoras Theorem Trigonometric Identities and Formulas by James Lowman Trigonometric identities are equations that are true for every value of the variable, or variables, that involve trigonometric functions




Trig Identity Sec2x Minus Tan2x T10 Youtube



Answered O Trigonometric Identities And Bartleby
Notebook Groups Cheat Sheets Sign In; = sin 2 x tan x sin 2 x double angle for sin 2x trig identity for tan x = 2sin xcos x sin x sin 2 x simplify cos x = 2 sin2 x sin 2 x = 3 sin 2 x = RHS (7) There are several ways to prove this Here is one solution LHS = (tan x – 1)(sin 2x – 2cos 2 x)7月 30, 21 Although these two functions look quite different from one another, they are in fact the same function This means that, for all values of x, This last expression is an identity, and identities are one of the topics we will study




Trigonometry Reciprocal Identities Expii




Trig Identities Maple Learn Maplesoft
2 Fit a rectangle inside a square while maintaining aspect ratio 4 Trig Identity Proof of Tan(x) Tan(y) 2 trigonometry of interfering waves 0 Addition of two simple periodic waves using Complex Sinusoidal forms Not making logical sense 1 Inversion ofIntegral of tan^2(x) How to integrate it step by step!👋 Follow @integralsforyou on Instagram for a daily integral 😉📸 @integralsforyou https//wwwinstag Explanation Change to sines and cosines then simplify 1 tan2x = 1 sin2x cos2x = cos2x sin2x cos2x but cos2x sin2x = 1 we have ∴ 1 tan2x = 1 cos2x = sec2x Answer link
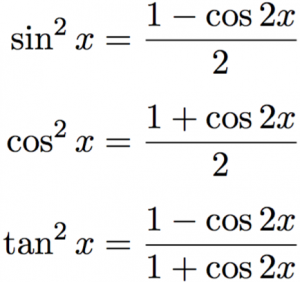



上 Tan2x Identity ただの悪魔の画像



What Is The Formula Of Tan2x Quora
Solved Prove The Following Trig Identity Sec 2 X 2secx Cosx Cos 2 X Tan 2 X Sin 2 X Course Hero Cos2x Identity Cos Sin Tan Csc Sec Cot Ppt Warm Up Powerpoint Presentation Free Download Id 3 Tangent Identities 1 1 Tan1 1 Tan2 1 Tan3 1 Tan45 2 N Brainly In Ryad Antonio Ebooks En Ligne Gratuit Double Angle Formula And Half Angle Formula Video Lessons Examples1tan2 x 2 2 cosx = 1−tan 2 x 2 1tan2 x 2 3 tanx = 2tan x 2 1−tan2 x 2 3 Less wellknown, but still useful identities First, from the doubling and sum formulas, it is easy to derive formulas for triple, quadruple, and so on angles For example 1 sin3x =3sinx −4sin3x 2 cos3x =4cos3x−3cosx 3 tan3x = 3tan x−tan3 1−3tan2xTrigonometric Identities are useful whenever trigonometric functions are involved in an expression or an equation Trigonometric Identities are true for every value of variables occurring on both sides of an equation Geometrically, these identities involve certain trigonometric functions (such as sine, cosine, tangent) of one or more angles Sine, cosine and tangent are
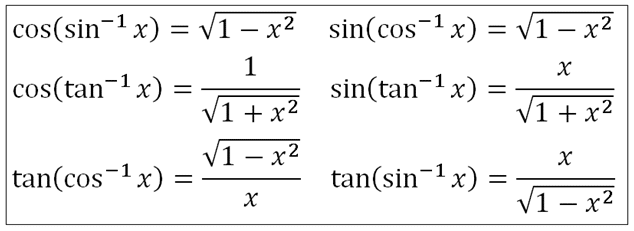



Inverse Trig Identities Reciprocal Of Trigonometric Function Trig




While You Wait Trigonometric Identities And Equations Section
Notebook Groups Cheat Sheets Sign In;Sin2x Cos 2x = 1 (trig identity) smxcosx smxcosx sm sm x —cos x x cos2 x smxcosx At this London school, math teachers, such as Henry, specialize m identifies trigonometry Dr Jekyll sin x cos x sin tan e — cose and, when discipline is an issue, they turn to Mr Hyde R Louis Stevenson Mathematics D epartment Teaching Identities R Louis Stevenson Mathematics DTan(2x) as tan(xx) So tan(2x)= 2tanx/1tanxtanx We can always go for the longer approch from sinx/cosx to derive this formula K views View upvotes 9 6 Sponsored by The Penny Hoarder 9 lessons from millionaires who are good with money Life would be a whole lot easier if someone would just Venmo us $1 million Read More Michael Osei, Student Mathematics & Science,



View Question Trig Identities Need Help




bestpictjcry Tan 2x Tan 2x
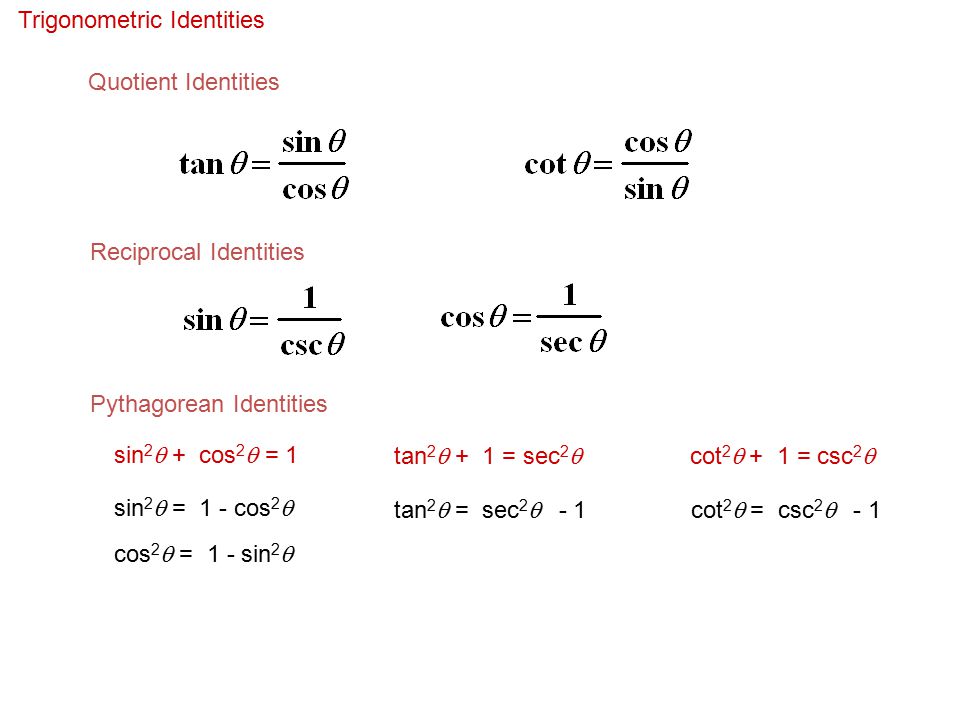
List of trigonometric identities 2 Trigonometric functions The primary trigonometric functions are the sine and cosine of an angle These are sometimes abbreviated sin θ) and cos(θ), respectively, where θ is the angle, but the parentheses around the angle are often omitted, eg, sin θ and cos θ The tangent (tan) of an angle is the ratio of the sine to the cosine Finally, theTrigonometric identities 18 Ma 2 MathRef Various identities and properties essential in trigonometry Legend x and y are independent variables, d is the differential operator, int is the integration operator, C is the constant of integration Identities tan x = sin x/cos x equation 1 cot x = cos x/sin x equation 2 sec x = 1/cos x equation 3 csc x = 1/sin x equation 4 cot x = 1/tanTo integrate tan^22x, also written as ∫tan 2 2x dx, tan squared 2x, (tan2x)^2, and tan^2(2x), we start by utilising standard trig identities to change the form of the integral Our goal is to have sec 2 2x in the new form because there is a standard integration solution for that in formula booklets that we can use We recall the Pythagorean trig identity, and multiply the angles by 2




How Do You Simplify 1 Tan 2 X 1 Tan 2 X Socratic



Www2 Math Binghamton Edu
Hyperbolic Trig Identities is like trigonometric identities yet may contrast to it in specific terms The fundamental hyperbolic functions are hyperbola sin and hyperbola cosine from which the other trigonometric functions are inferred You can easily explore many other Trig Identities on this website So here we have given a Hyperbola diagram along these lines giving you thought Finally, all we need to do now is derive the tangent double angle formula Like the previous examples, change the B's to A's in the addition formula for tangent tan (AB) = (tanA tanB)÷ (1 – tanAtanB) tan (AA) = (tanA tanA)÷ (1 – tanAtanA) tan(2A) = (2tanA) ÷ (1 tan²A) So there you have the 3 double angle trigonometric trigonometric identities tan^2 3869Trigonometric identities tan^2 リンクを取得 ;




Solved 5 2 Verify The Following Trigonometric Identities A Chegg Com
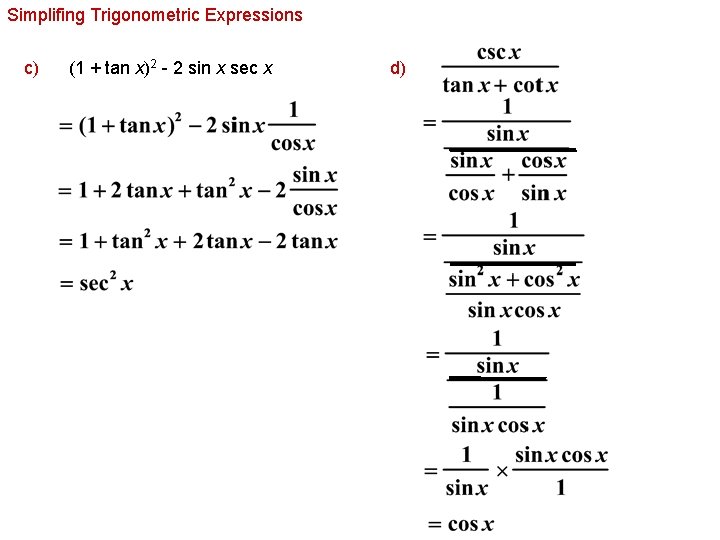



While You Wait Trigonometric Identities And Equations Section
Simplify trigonometric expressions Calculator online with solution and steps Detailed step by step solutions to your Simplify trigonometric expressions problems online with our math solver and calculator Solved exercises of Simplify trigonometric expressionsThere are some trigonometric identities which you must remember in order to simplify trigonometric expressions when required These are \{\sin ^2}x {\cos ^2}x = 1\The algebraic identities relate just the variables whereas the trig identities relate the 6 trigonometric functions sine, cosine, tangent, cosecant, secant, and cotangent Let's learn about each type of trigonometric identities in detail Reciprocal Trigonometric Identities We already know that the reciprocals of sin, cosine, and tangent are cosecant, secant, and cotangent




Trig Identities Bingo Card
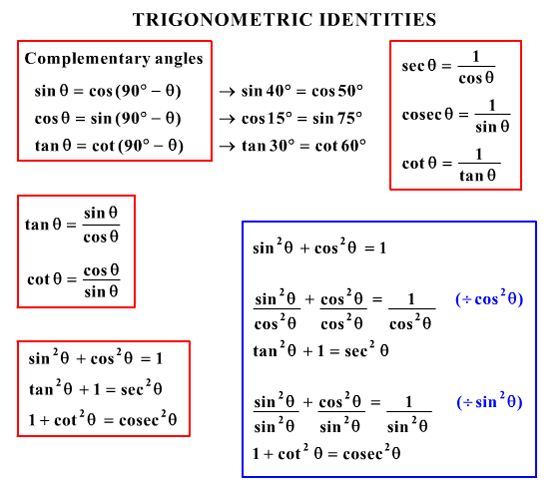



What Would Be Steps In Proving That Tan2x Secx 1 1 Sec X Socratic
Basic Trig Identities The basic trig identities or fundamental trigonometric identities are actually those trigonometric functions which are true each time for variablesSo, these trig identities portray certain functions of at least one angle (it could be more angles) It is identified with a unit circle where the connection between the lines and angles in a Cartesian planeCos 2x is an important identity in trigonometry which can be expressed in different ways It can be expressed in terms of different trigonometric functions such as sine, cosine, and tangentCos 2x is one of the double angle trigonometric identities as the angle in consideration is a multiple of 2, that is, the double of x•use trigonometric identities to integrate sin2 x, cos2 x, and functions ofthe formsin3x cos4x •integrate products of sines and cosines using a mixture of trigonometric identities and integration by substitution •use trigonometric substitutions to evaluate integrals Contents 1 Introduction 2 2 Integrals requiring the use of trigonometric identities 2 3 Integrals involving




How Do You Prove The Identities Cosx Secx Sinx Cscx Sec 2x Tan 2x Socratic




Tan2x Please Help This Is My Final I Can T Fail It Brainly Com
Tan(x y) = (tan x tan y) / (1 tan x tan y) sin(2x) = 2 sin x cos x cos(2x) = cos ^2 (x) sin ^2 (x) = 2 cos ^2 (x) 1 = 1 2 sin ^2 (x) tan(2x) = 2 tan(x) / (1 The following are the identities of inverse trigonometric functions sin1 (sin x) = x provided (1 – x 2)/x Therefore, tan(cos1 x) = tan(tan1 √(1 – x 2)/x ) = √(1 – x 2)/x Question 4 tan1 √(sin x) cot1 √(sin x) = y Find cos y Solution We know that tan1 x cot1 x = /2 therefore comparing this identity with the equation given in the question we get y = π /2



Pythagorean Identities



Trig Identities Hsn Forum
.JPG)



Every Day I M Calculatin I D3 Unit Q Pythagorean Identities




Ppt Basic Trig Identities Sin 2 X Cos 2 X 1 Powerpoint Presentation Id




Tan2x 2tanx 1 Tan X Trigonometric Identity Solve Hindi Youtube
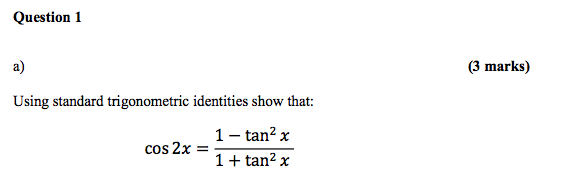



Solved A Using Standard Trigonometric Identities Show That Chegg Com




Which Of The Following Equations Are Identities Check All That Apply A Cot 2x Csc2x 1 B Brainly Com




Integrate Sec 2x Method 1
x-1=sec(squared)x.jpg)



10 Identity Tan Squared X 1 Sec Squared X Trigonometry Educator Com




Tan 2x Formula What Is Tan 2x Formula Examples
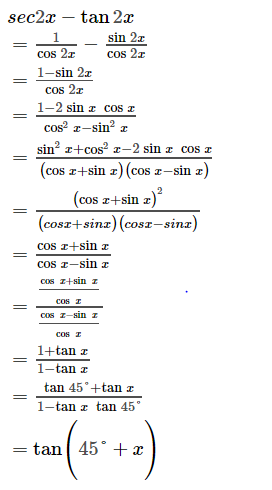



Sec2x Tan2x If0 X P 4




Solved Verify That The Equation Is An Identity Tan 2x Cot Chegg Com



What Is The Formula Of Tan2x Quora




How To Solve Tan 2xsin 2x Tan 2x Sin 2x Trigonometry Trigonometric Identities Youtube




Analytic Trig Ppt Video Online Download




How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Socratic




Cos 2x Formula Derivation Examples What Is Cos 2a Formula



Math Brown Edu




Tan2x ただの悪魔の画像




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo
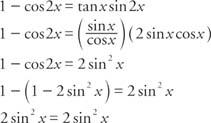



Double Angle And Half Angle Identities




Trig Double Identities Trigonometric Double Angle Functions Trig




List Of Trigonometric Identities Wikipedia




Trigonometry Identity Tan 2 X 1 Sec 2 X Youtube




70pmylqshcbm




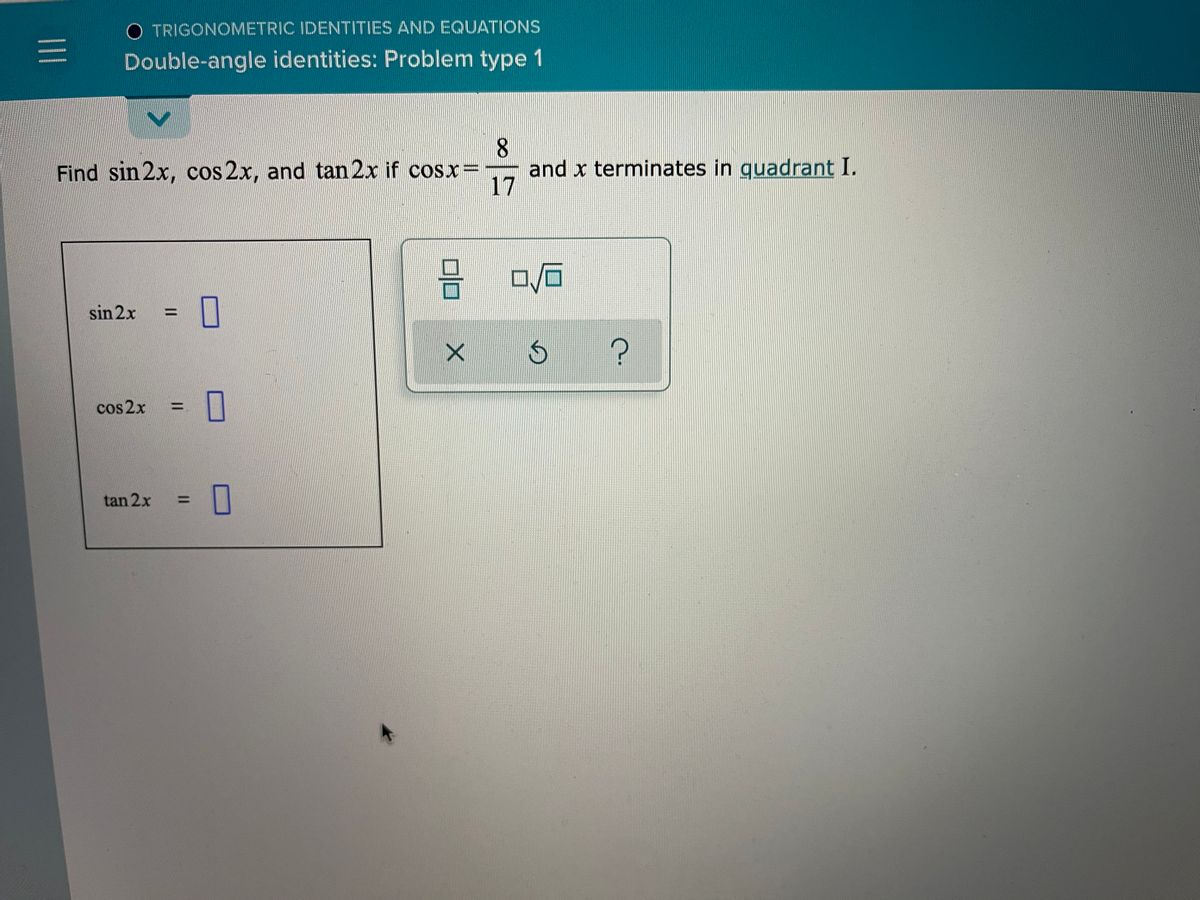
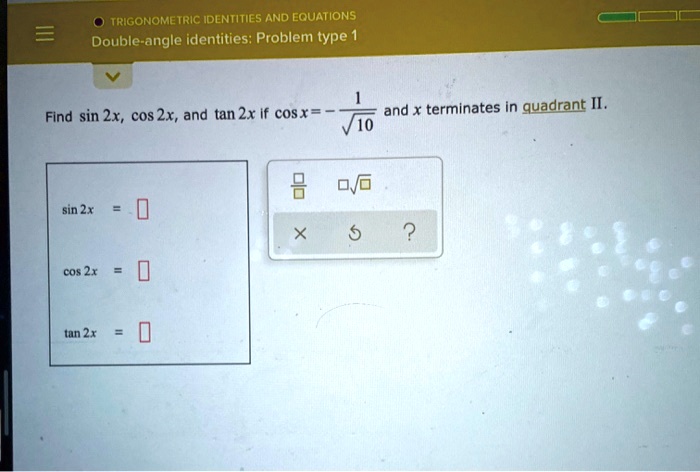
O Trigonometric Identities And Equations Double Angle Identities Problem Type 1 3 Find Sin 2x Cos 2x Homeworklib




How To Use Trig Identities Mathematics Stack Exchange



Trigonometric Identities Learn Trigonometry By Ib Elite Tutor



Cos2x Identity




Sin X 2 Tan X 2 1 Tan 2 X 2 Eraoco




Precalculus Trigonometry Trig Identities 29 Of 57 Formula For Lowering Power Tan 2 X Youtube




How Do You Simplify Sec 4x Tan 4x Sec 2x Tan 2x Socratic




Using Trigonometric Identities Video Khan Academy




How Do You Use The Fundamental Trigonometric Identities To Determine The Simplified Form Of The Expression Socratic



Trig Identities Crossword Wordmint



3
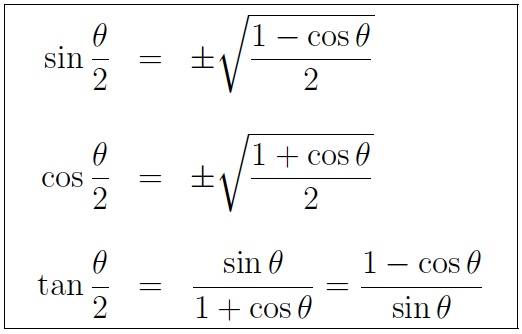



Trig Identities Table Of Trigonometric Identities



6 1 2 Trigonometric Identities




Lesson 4 5 Double Angle Formulas



A Trig Identity



Shsu Edu



Solved Prove Trigonometric Identities Course Hero




Tan2x Tan 2x Identity For Tan2x Proof Of Tan2x Identity Formula For Tan2x Youtube




How To Use Double Angle Identities Studypug
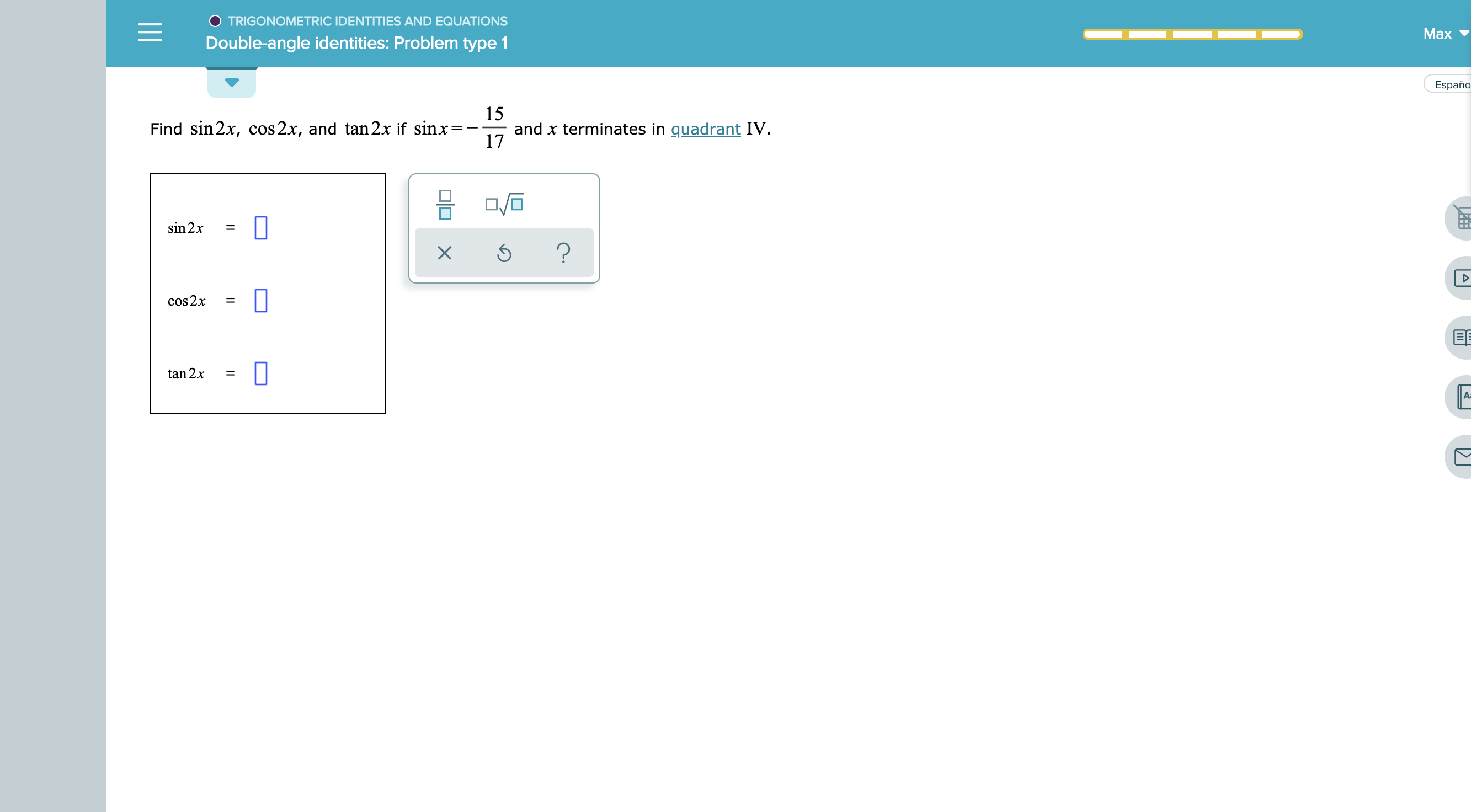



Answered O Trigonometric Identities And Bartleby




Tan2x 2tanx 1 Tan X Trigonometric Identity Solve Hindi Youtube



Ilectureonline




Solved Using Standard Trigonometric Identities Show That Chegg Com




Trig Identities Bingo Card




Show That The Following Are Not Trigonometric Identities 1 Tan 2x 2tan X 2 Sec X Sqrt 1 Tan 2 X 3 Sin X Y Sin X Sin Y Study Com



Solved Prove The Following Trig Identities Course Hero



Xehqmdugm2kwhm




Integrate Tan 2x




Sum And Difference Identities Video Lessons Examples And Solutions




Trigonometric Identities And Examples With Worksheets




Warm Up Prove Sin 2 X Cos 2 X 1 This Is One Of 3 Pythagorean Identities That We Will Be Using In Ch 11 The Other 2 Are 1 Tan 2 X Sec 2 X Ppt Download




9 1 Identities And Proofs Ppt Download




Verifying A Trigonometric Identity Tan 2 X 1 Sec X Sec X Youtube




Tangent Half Angle Formula Wikipedia



Biomath Trigonometric Functions




Sat Math Flashcards Quizlet




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo



7 Proving Ids Trig Functions Identities




What Is The Integration Of Tan 2x Solution Quora




Warm Up Prove Sin 2 X Cos 2 X 1 This Is One Of 3 Pythagorean Identities That We Will Be Using In Ch 11 The Other 2 Are 1 Tan 2 X Sec 2 X Ppt Download



Trigonometric Identities Cheat Sheet Doubleroot In



Math Problems Simplifying With Trigonometry Identities And Then Integration




Tan2x ただの悪魔の画像



Solved Prove The Following Trig Identity Sec 2 X 2secx Cosx Cos 2 X Tan 2 X Sin 2 X Course Hero



11 Basic Trigonometric Identities An Identity Is An Equation That Is True For All Defined Values Of A Variable We Are Going To Use The Identities To Ppt Download



View Question For Questions 1 5 Decide Whether The Equation Is A Trigonometric Identity Explain Your Reasoning



1




Solved Inquiry 11 8 Marks Prove The Following Trig Chegg Com




5 1 Fundamental Trig Identities Reciprocal Identities Sin



Bestmaths Online Proof 4



Tan2x ただの悪魔の画像



Trigonometric Identities All In One Cheat Sheet Docsity
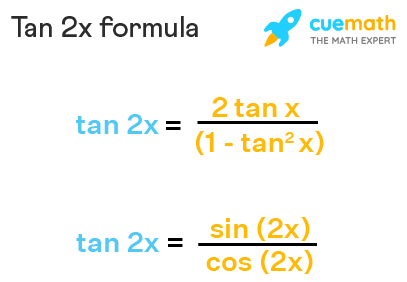



Tan 2x Formula What Is Tan 2x Formula Examples



0 件のコメント:
コメントを投稿