We draw a graph of tanu over this interval as shown in Figure 4 90 180 360 5401 135 315 495 1 45 tan€ u u o o o o Figure 4 A graph of tanu We know from the Table on page 2 that an angle whose tangent is 1 is 45 , so using the symmetry in the graph we can find the angles which have a tangent equal to −1 The first will be the sameFree online tangent calculator tan(x) calculator This website uses cookies to improve your experience, analyze traffic and display adsSolving trigonometric equations in radians (extension) To solve trigonometric equations involving radian measure, you should proceed in the same way as for degrees
Solution How To Find The Number Of Cycles In 2pi The Horizontal Length Of Each Of The 4 Quadrants Of Each Cycle The Horizontal Shift Of Each Cycle F X Tan 2x 3
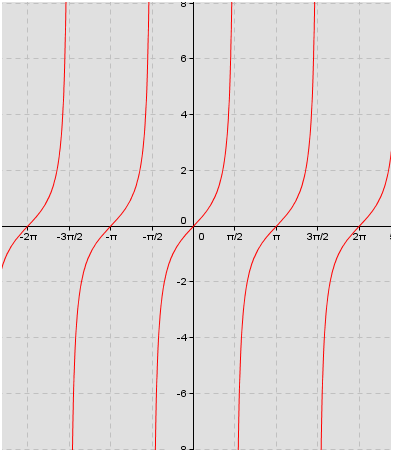
Tan 2x graph radians
Tan 2x graph radians-To graph the tangent function, the angle is marked on xaxis (either in degrees or radians) and the corresponding tangent value of the angle is marked on yaxis The resulting graph extends to positive infinity in one direction and negative infinity in the otherThe answer is as follows Tan(2) = This is the same answer you will get if you have a scientific calculator set to RAD mode and then enter 2 followed by the Tan button To find tan of another number, please enter the number below and press "Calculate Tan"



Graphing Tangent Read Trigonometry Ck 12 Foundation
Frequency and period are related inversely A period #P# is related to the frequency #f# # P = 1/f# Something that repeats once per second has a period of 1 s It also have a frequency of # 1/s#One cycle per second is given a special name Hertz (Hz)Graph y=tan(2x) Find the asymptotes Tap for more steps For any , vertical asymptotes occur at , where is an integer Use the basic period for , , to find the vertical asymptotes for Set the inside of the tangent function, , for equal to to find where the vertical asymptote occurs forJan 02, 21 · In other words, the graph of the cosine function is just the graph of the sine function shifted to the left by \(90^\circ = \pi/2 \) radians, as in Figure 515 Figure 515 Graph of \(y = \cos x\) To graph the tangent function, use \(\tan\;x = \frac{\sin\;x}{\cos\;x} \) to get the following graph Figure 516 Graph of \(y = \tan x\)
Tangent of argument in radians collapse all in page Syntax Y = tan(X) Description example Y = tan(X) returns the tangent of each element of X The tan function operates elementwise on arrays The function accepts both real and complex inputsThe period of the tangent graph is π radians, which is 0° to 180° and therefore different from that of sine and cosine which is 2π in radians or 0 to 360° Recall that and cosx has a value of 0 when x= 90° or 270° This can create a situation in which the denominator will be zero and therefore undefined when using the tangent functionGraphing Trig Functions Review Worksheet Give the period, amplitude, and quarter points for each graph (use radians) DO NOT GRAPH!!
Notation Several notations for the inverse trigonometric functions exist The most common convention is to name inverse trigonometric functions using an arc prefix arcsin(x), arccos(x), arctan(x), etc (This convention is used throughout this article) This notation arises from the following geometric relationships citation needed when measuring in radians, an angle of θ radiansMay 09, 16 · Here's the graph (mousewheel to zoom) graph{tan(2x) 5, 5, 25, 25} The graph is just like tan(x), but 2 times faster It has period pi/2 The roots are at npi/2 for all integers n and graph has slope 2 at these points The asymptotes are at (n1/2)pi/2 More info here Generally for any fancy function f(x) we can think of its internal clock (as if it is function of time) For realRound your answer to the nearest hundredth of a radian D 085 Which is equivalent to cos^1(017)?


Solution How To Find The Number Of Cycles In 2pi The Horizontal Length Of Each Of The 4 Quadrants Of Each Cycle The Horizontal Shift Of Each Cycle F X Tan 2x 3
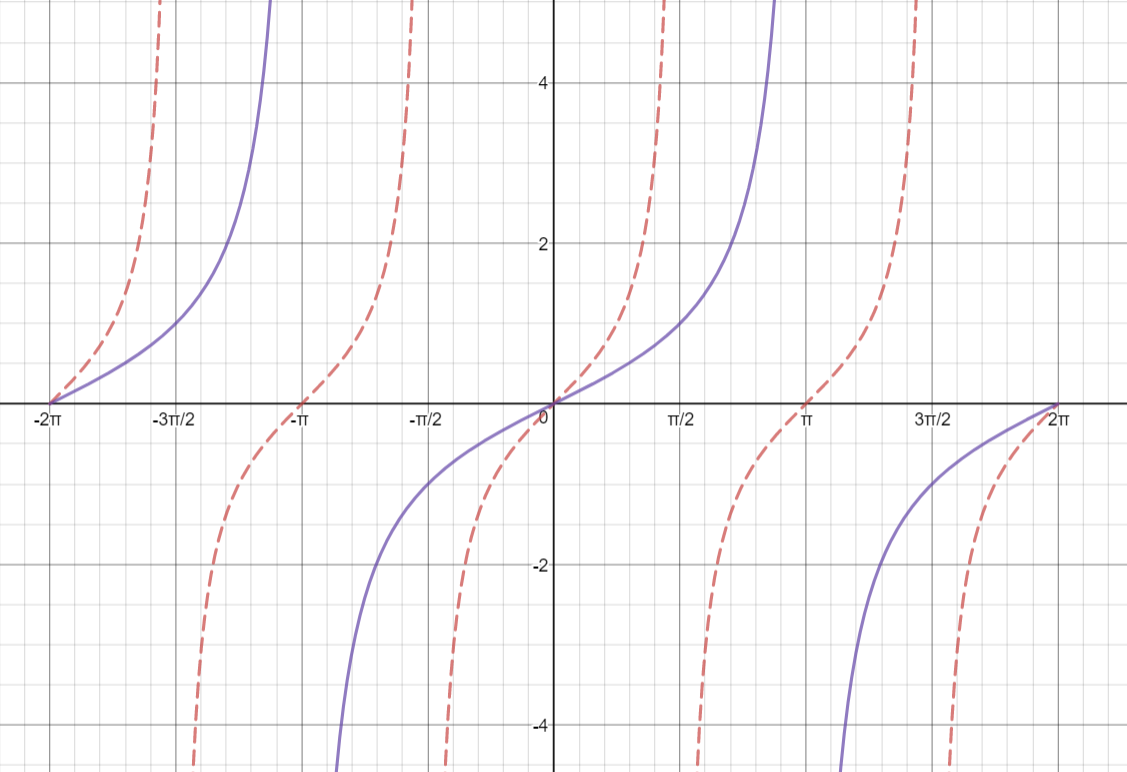


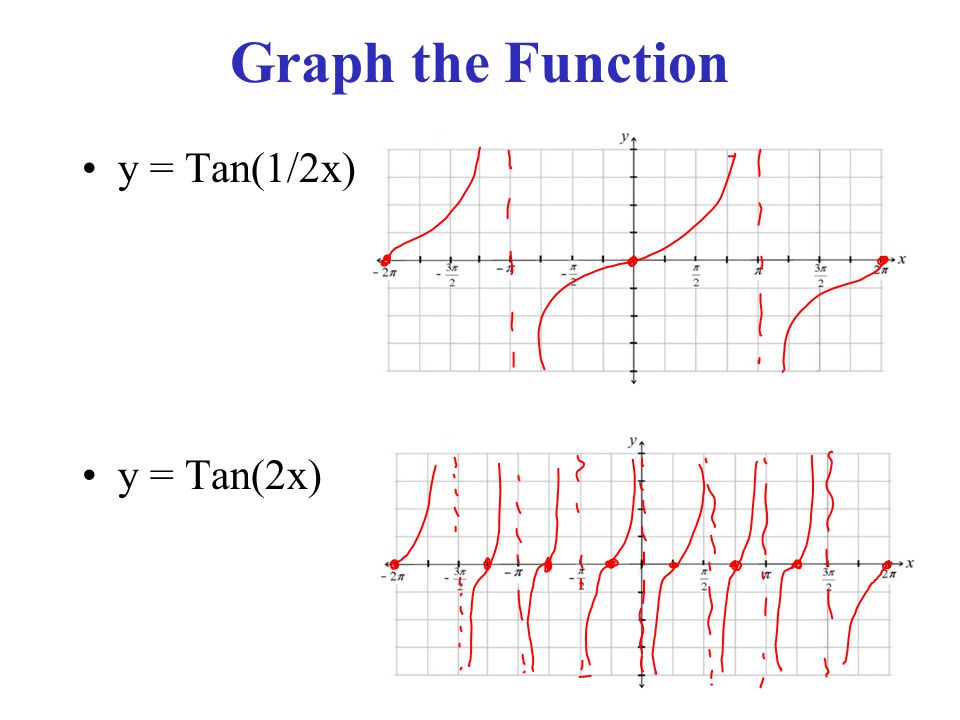
How Do You Graph Y Tan 1 2 X Socratic
Related » Graph » Number Line » Examples » Our online expert tutors can answer this problem Get stepbystep solutions from expert tutors as fast as 1530 minutesJan 02, 21 · The functions sin x, cos x, csc x, and sec x all have the same period 2 π radians We saw in Section 51 that the graphs of y = tan x and y = cot x repeat every 2 π radians but they also repeat every π radians Thus, the functions tan x and cot x have a period of π radiansOct 17, 14 · Look at the example below Figure ( i) A tangent graph has a period of 90o or π/2 radians Meaning a new tangent graph starts after 90o or π/2 every Radians Degrees An easy way to remember, look at the part of wave circled, they look like 2 half circles (semicircles) 2 semicircles make one complete circle


Graph Tangent And Cotangent


Math Scene Trigonometry Functions Graphs Of Trig Functions Lesson 3
Textbook solution for Precalculus (MindTap Course List) 10th Edition Ron Larson Chapter 46 Problem 2CP We have stepbystep solutions for your textbooks written by Bartleby experts!To be able to graph trigonometric functions using radians as angles The first function we will graph is the sine function We will describe a geometrical way to create the graph, using the unit circleThis is the circle of radius 1 in the xyplane consisting of all points (x, y) which satisfy the equation x 2 y 2 = 1 We see in Figure 1 that any point on the unit circleRadians/Degrees Degrees to radians mult by 180 Radians to degrees mult by 180 To quickly change to degrees while in radian mode, use the degree



The Sine Cosine And Tangent Functions
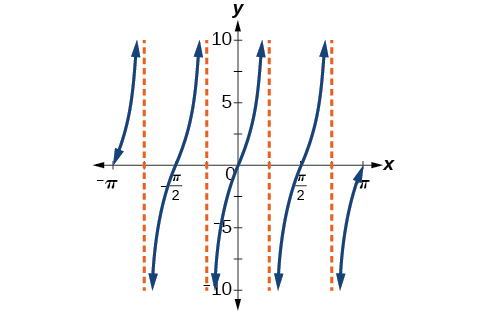


Graphs Of The Other Trigonometric Functions Algebra And Trigonometry
Sketch the graph using radians by creating a table of coordinate pairs using domain 2x to 2x, one value every radians Then identify the amplitude and the period of each function 1) y=sino 2) y=cos @ 3) y =tanIII Check yourself Sketch (by hand!) what the graph of y = tanx will look like, given the following domain restrictions Be careful about where the graph crosses the xaxis, where the points of inflection are, and where the asymptotes are a) 2p to 4p b)4p to 0 c)3p/2 to p/2Jun 28, 14 · TAN to 90 degrees (PI/2 Radians) is 1/0, which is undefined, so you can't graph a result that's not there You can get as close as you want to 90 degrees,



Howto How To Find Vertical Asymptotes Of Tan2x
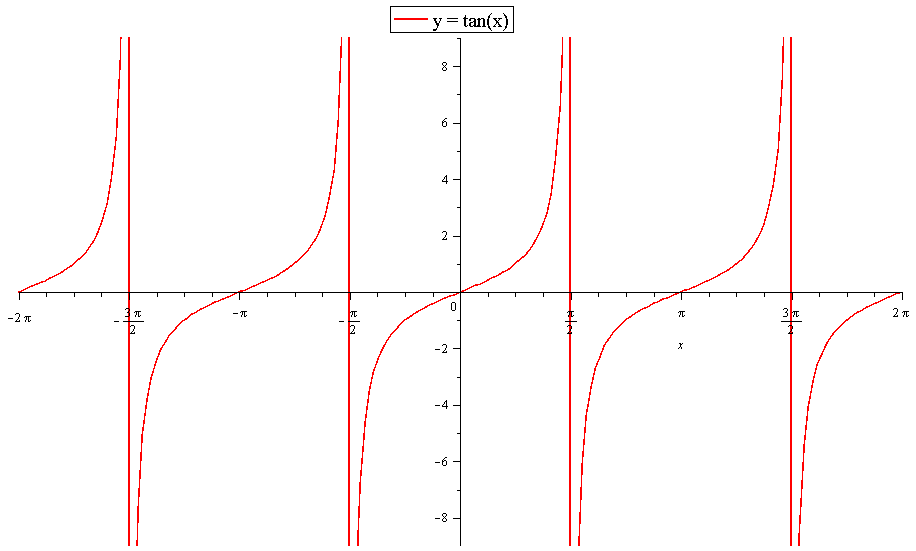


How Do You Graph Y Tan3x Socratic
Plot the points and join with a smooth curve Example The diagram shows a graph of y = tan x for 0˚ ≤ x ≤ 360˚, determine the values of p, q and r Solution We know that for a tangent graph, tan θ = 1 when θ= 45˚ and 225˚So, b = 45˚ We know that for a tangent graph, tan θ = 0 when θ= 0˚, 180˚ and 360˚So, c = 180˚ Graphing the Tangent FunctionPress GRAPH 5 Change Y 2T = cos T to examine cosine Save This Sheet !A cycle of a tangent is the graph between the asymptotes For the middle cycle, the asymptotes are x = ±π/2 A period is the width of a cycle So the period of y = tan x is π/2 (π/2) = π
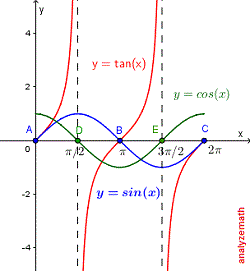


Graph Tangent And Cotangent



How To Graph Tan Cot Sec And Csc Obedchem
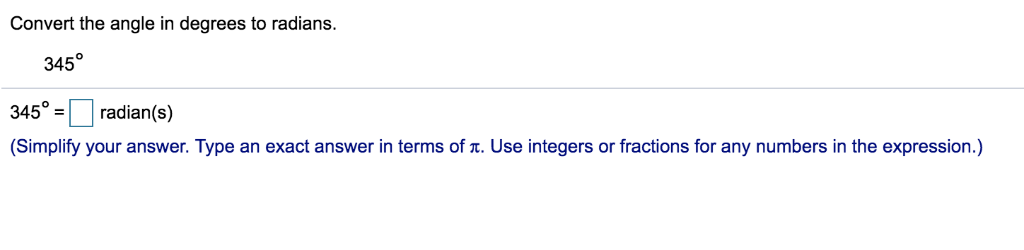
6) Find the measure (in radians) of a central angle of a sector of area 46 square inches in a circle of radius 5 inches Round to the nearest hundredth 6) A) 184 radians B) 736 radians C) 552 radians D) 368 radians 7) A pendulum swings through an angle of 5° each second If the pendulum is 11 cm in length andApr 15, 21 · Trigonometric Functions are formed when trigonometric ratios are studied in terms of radian measure for any angle (0, 30, 90, 180, 270)These are also defined in terms of sine and cosine functions In this article, we will provide you with all the details on trigonometric functions such as value in degree, radians, complete trigonometric table and other relevant informationConvert between degree and radian measures B11, 12 L2 Trig Ratios and Special Angles Determine, without technology, the exact values of trig ratios for special angles B13, 14 L3 Graphing Trig Functions sketch the graphs of all 6 trig ratios and be able to describe key properties B21, 22, 23 L4 Transformations of Trig Functions


Trigonometry Trigonometric Functions


Solution Show Me The Graph Of Y Tan2x Step By Step And How To Solve Keypoints
Online arctan(x) calculator Inverse tangent calculatorEnter the tangent value, select degrees (°) or radians (rad) and press the = buttonDo tangent graphs have "amplitude?" Why or why not?Find the amplitude, the vertical asymptotes in radian, the phase shift in radians, the vertical shift, and sketch the graph {eq}y = 4 \tan \left( 2x \dfrac{ \pi}{2}\right) 2 {/eq}
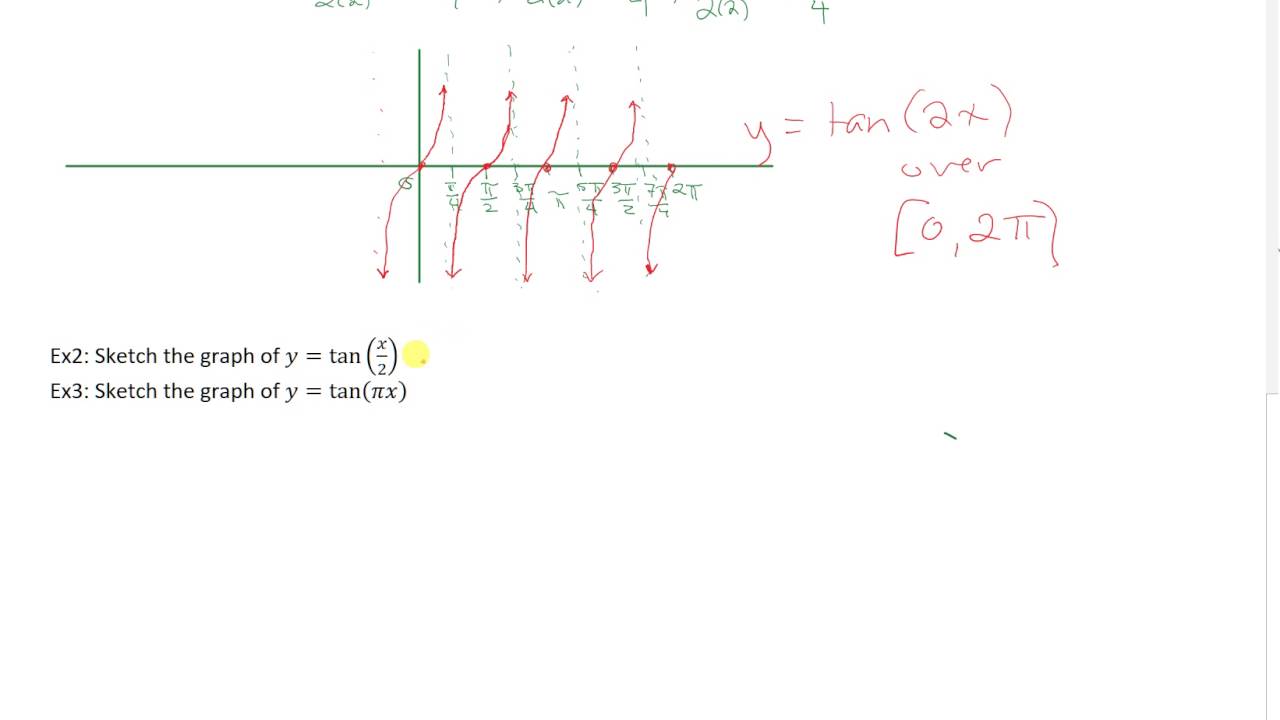


Sketching Y Tan 2x And Y Tan X 2 Youtube


Solution Graph Y 1 2 Tan 2x Pi 2 And The Period And Phase Shift
The other four trigonometric functions (tan, cot, sec, csc) can be defined as quotients and reciprocals of sin and cos, except where zero occurs in the denominator It can be proved, for real arguments, that these definitions coincide with elementary geometric definitions if the argument is regarded as an angle given in radiansCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyHere's a graph of y = tan (2x) as you can see, the pattern repeats every pi/2 radians here's a graph of y = tan (2x) the pattern repeats every pi/2 radians and the pattern is reversed from top to bottom because the frequency is minus 1 rather than plus one



6 Trigonometry Graph Example 3 Sketch Y Tan 2x Youtube



Math 127 Final Review Sheet Graphing Angles And Radian Measure
Round your answer to the nearest hundredth of a radian What are all the exact solutions of 2sin^2x sinx = 0 for 0Graphing Tangent Functions Name_____ Date_____ Period____ ©V s2o0M1^8U qKluxtxay TSWofBtSwNamrweq tLtL`CtS E dAHl\l` IrFiQgCh^txsy \rFeqsqeCrBvaecd1Find the period in radians, the phase shift in radians, and the vertical shift Then sketch the graph using radians 1) y = tan q 3 p 2 p3p 2 2p5p 2 3p7p 2 4p9pHere we answer one simple question What is tan (2) radians?
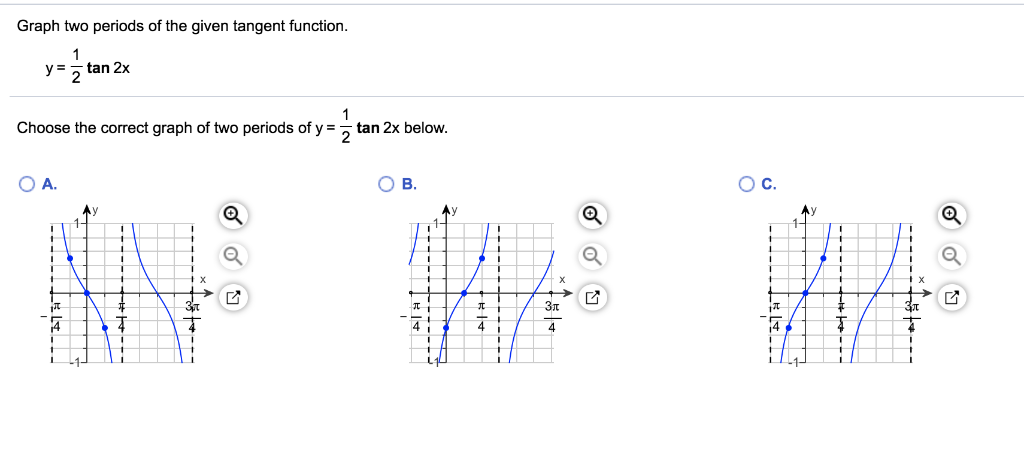


Solved Graph Two Periods Of The Given Tangent Function Y Chegg Com



Trigonometry Graphs For Sine Cosine And Tangent Functions
Decimal to Fraction Fraction to Decimal Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time StepbyStep Calculator sec^2xtan^2xcot^2x1 y = 3 sin (2x) 2 y = 4 cos 3 y = 5 sin 4 y = 7 cos 1 5 y = 4 tan 6 y = 2 cot Write an equation of the givenSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more



Graphs Of Trigonometric Functions Sine Cosine Tangent Etc


What Is The General Solution Of X For Tan X Tan2x 1 Quora
From what I know about the graph of the tangent, I know that the tangent will equal 1 at 45° after every 180° These solutions for tan( x /2) are at 0° 45°, 180° 45°, 360° 45° , and so forthArcsin Arcsine, written as arcsin or sin1 (not to be confused with ), is the inverse sine function Sine only has an inverse on a restricted domain, ≤x≤In the figure below, the portion of the graph highlighted in red shows the portion of the graph of sin(x) that has an inverseThis video shows how to graph the cosine, sine, and tangent functions using desmoscomhttp//mathispower4ucom



Aim What Are The Graphs Of Tangent Function And Reciprocal Functions Ppt Download
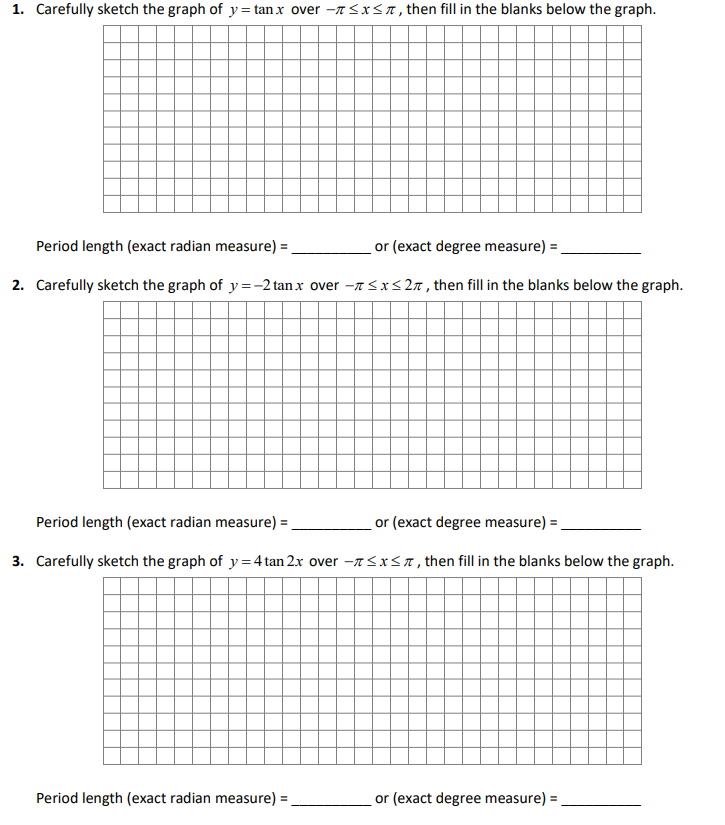


Solved 1 Carefully Sketch The Graph Of Y Tan X Over 1 Chegg Com
Subsection The Tangent Function The transformations of shifting and stretching can be applied to the tangent function as well The graph of \(y=\tan x\) does not have an amplitude, but we can see any vertical stretch by comparing the function values at the guidepoints Example 712 Graph \(y=13\tan 2x\text{}\)TAN function Description Tangent function TAN(x) returns the tangent of the angle xThe argument x must be expressed in radians To convert degrees to radians you use the RADIANS function The tangent can be represented in terms of sine and cosineTangent of argument in radians collapse all in page Syntax Y = tan(X) Description example Y = tan(X) returns the tangent of each element of X The tan function operates elementwise on arrays The function accepts both real and complex inputs
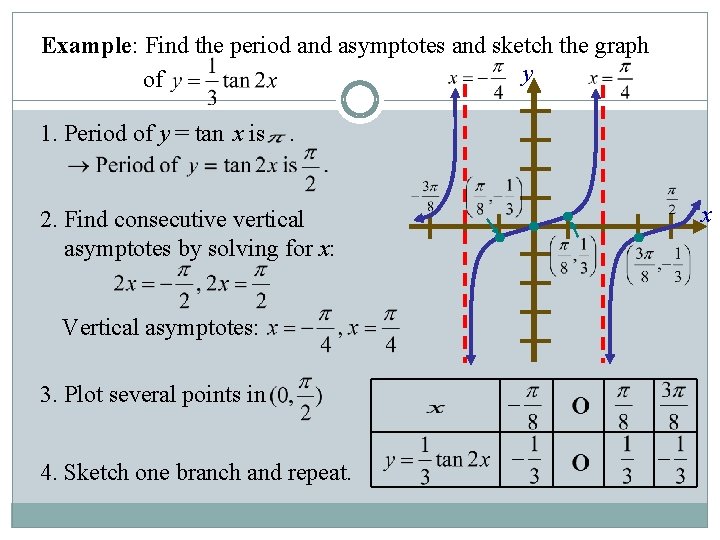


Trigonometric Functions Graphing The Trigonometric Function Graphing Trigonometric


Tangent Graphs


Biomath Trigonometric Functions



Graphing The Tangent Function Amplitude Period Phase Shift Vertical Shift Video Lesson Transcript Study Com



Graphing Tangent Read Trigonometry Ck 12 Foundation



Investigating Y Sin Bx And Y Tan Bx 14murayu



Graphing Tangent Read Trigonometry Ck 12 Foundation
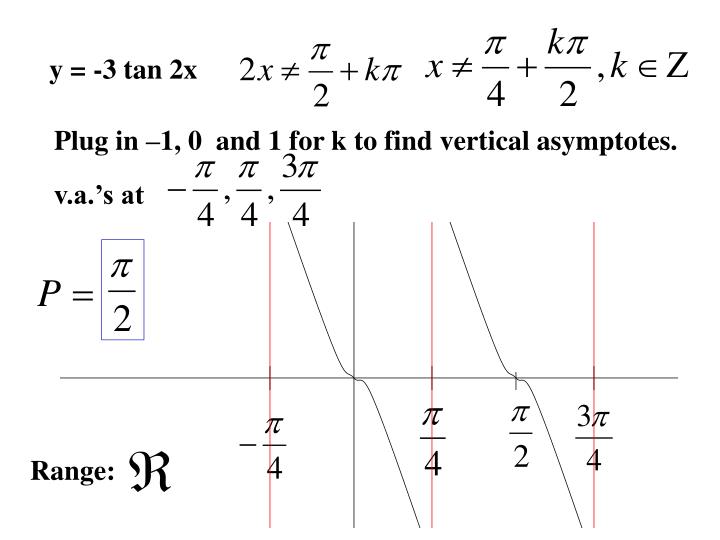


Howto How To Find Vertical Asymptotes Of Tan2x



Trig Solving Equations



Solved Solve Finding All Solutions Express Your Answer Chegg Com
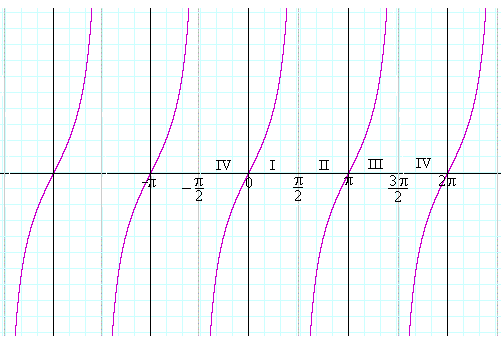


Graphs Of Trigonometric Functions


Solution Determine The Period Of Y Tan 2x
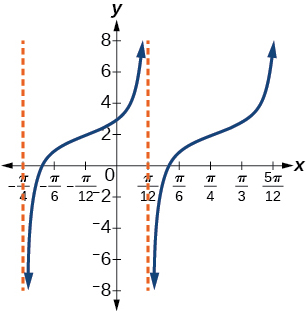


Graphs Of The Other Trigonometric Functions Algebra And Trigonometry
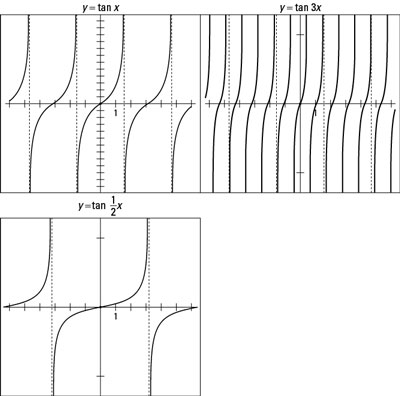


Graph Tangent Functions With Variable Multipliers Dummies
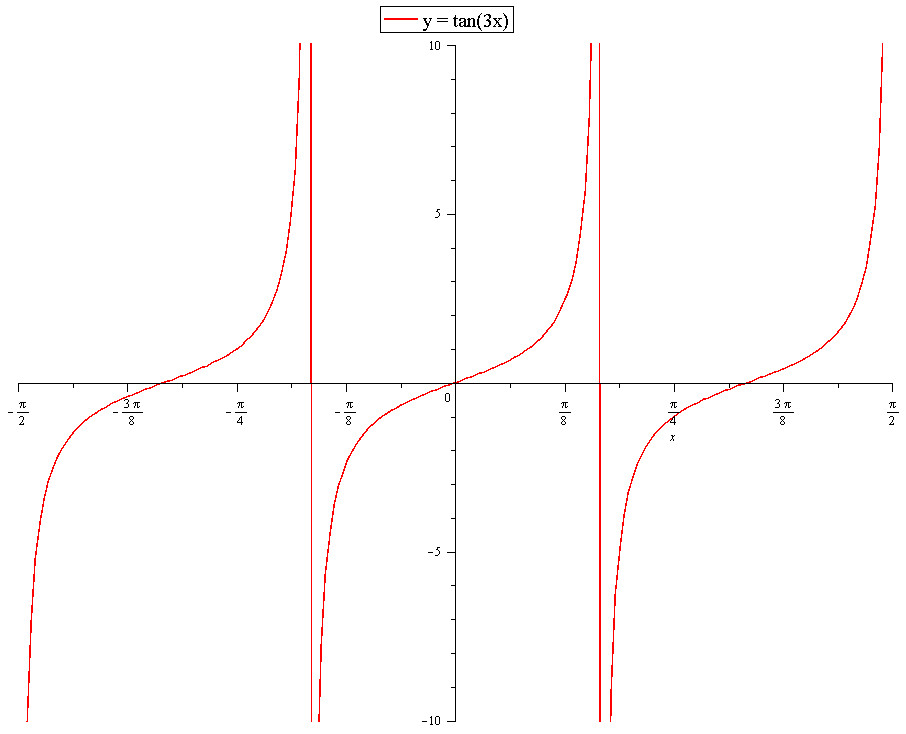


How Do You Graph Y Tan3x Socratic
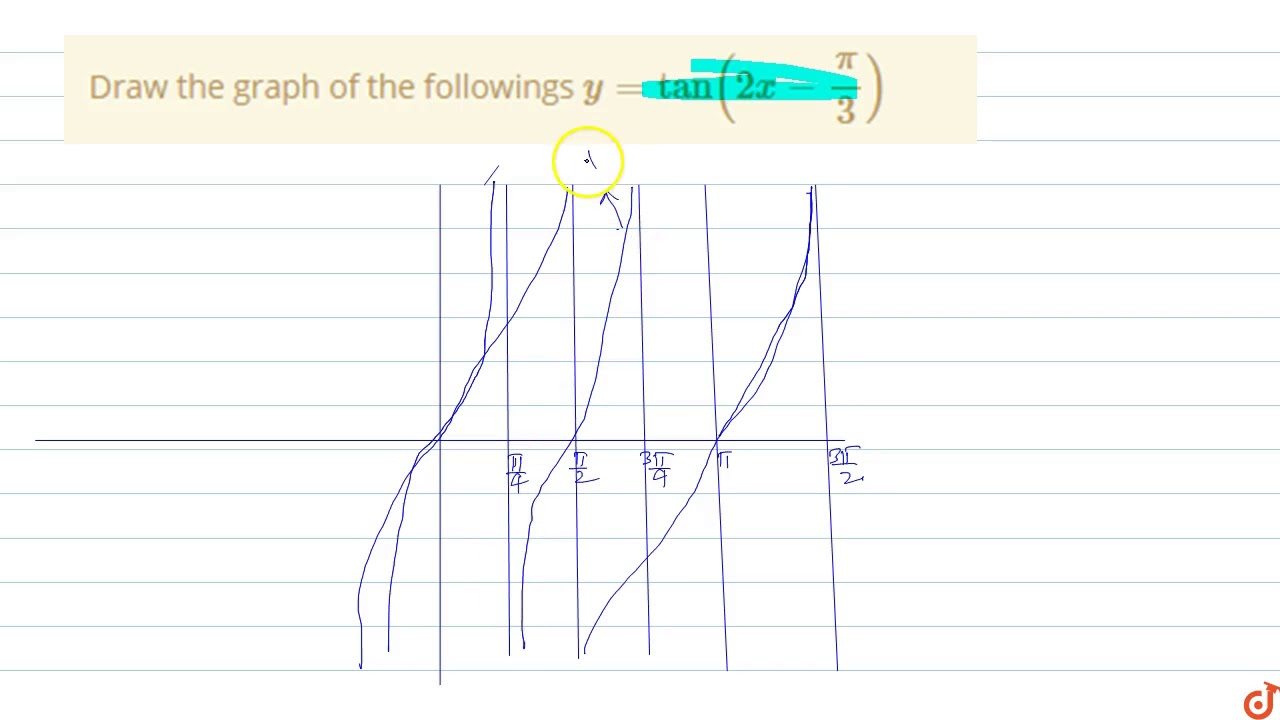


Draw The Graph Of The Followings Y Tan 2x Pi 3 Youtube


Trigonometry Functions User S Blog
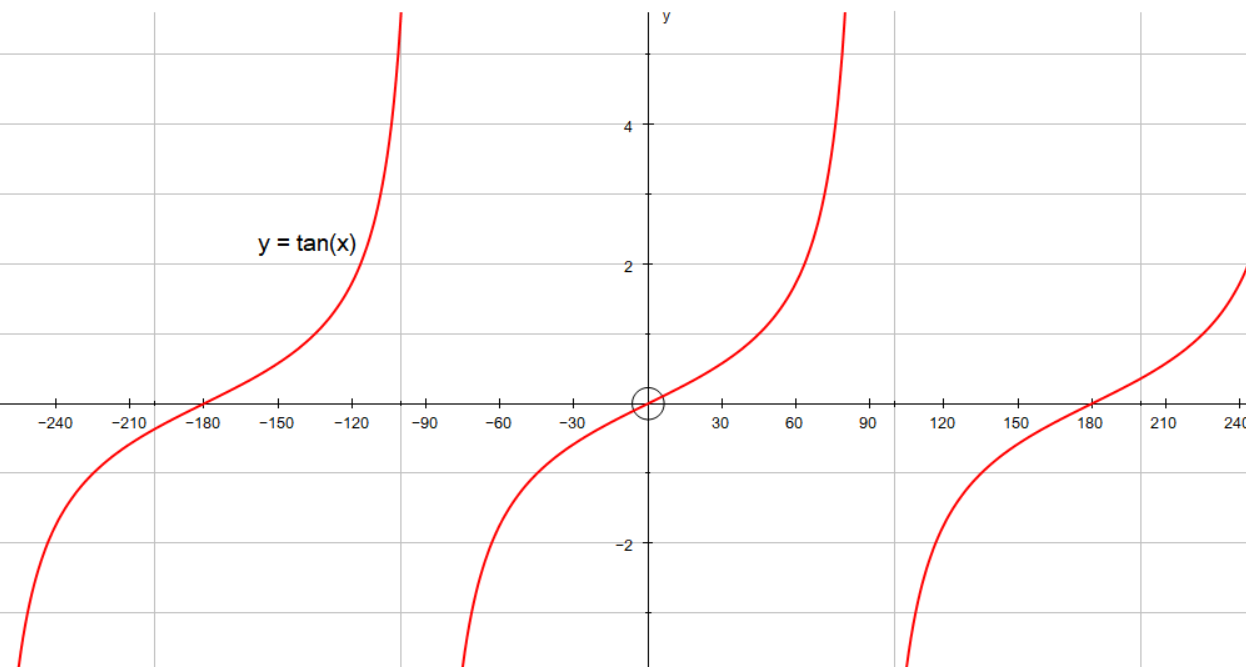


How Do You Graph And List The Amplitude Period Phase Shift For Y Tan X 60 Socratic
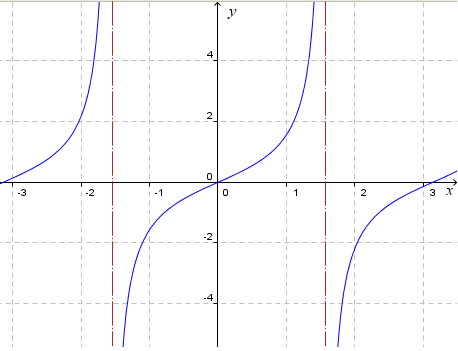


Explore The Slope Of The Tan Curve



Trigonometric Functions


Solution Determine The Period Of Y Tan 2x



Graph Y Tan 2x Youtube
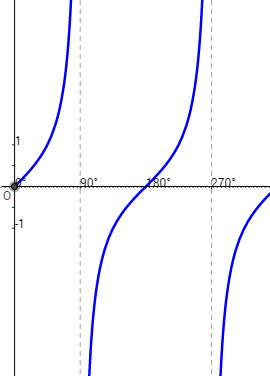


Sine Cosine Tangent Graphs Video Lessons Examples And Solutions
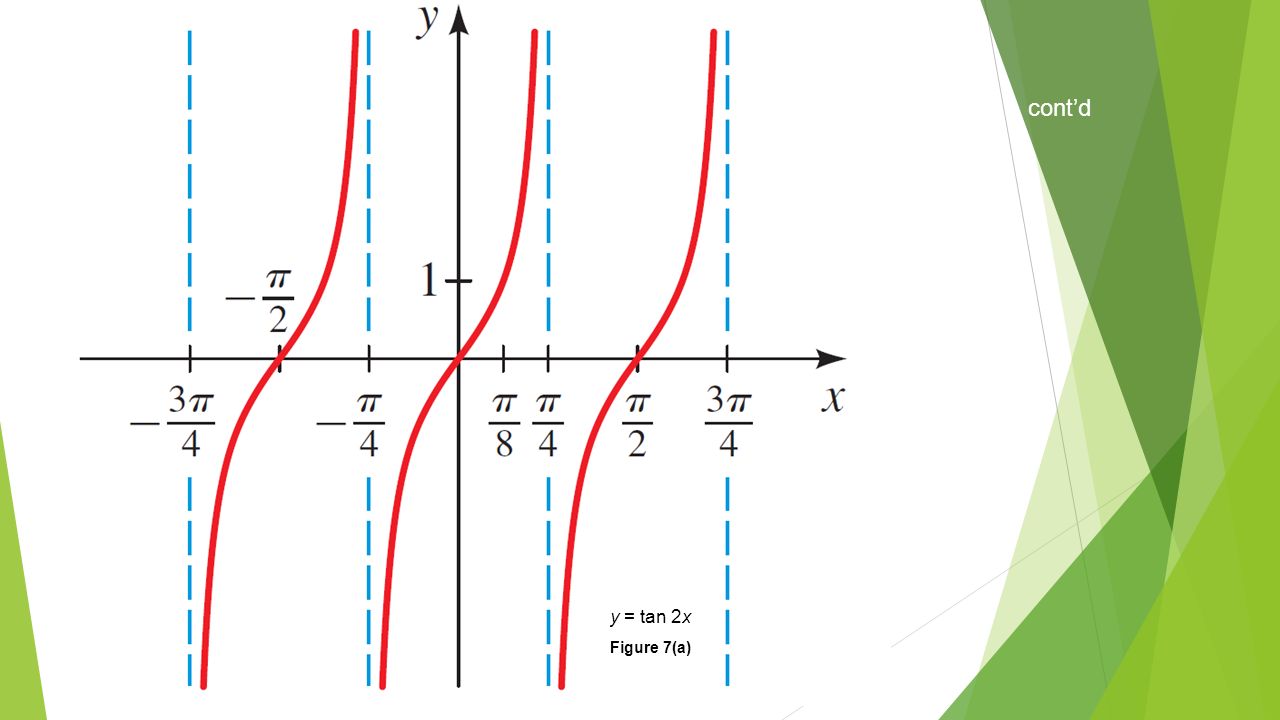


Tan2x ただの悪魔の画像
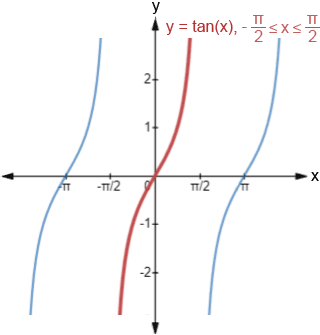


Arctan



The Squeeze Theorem
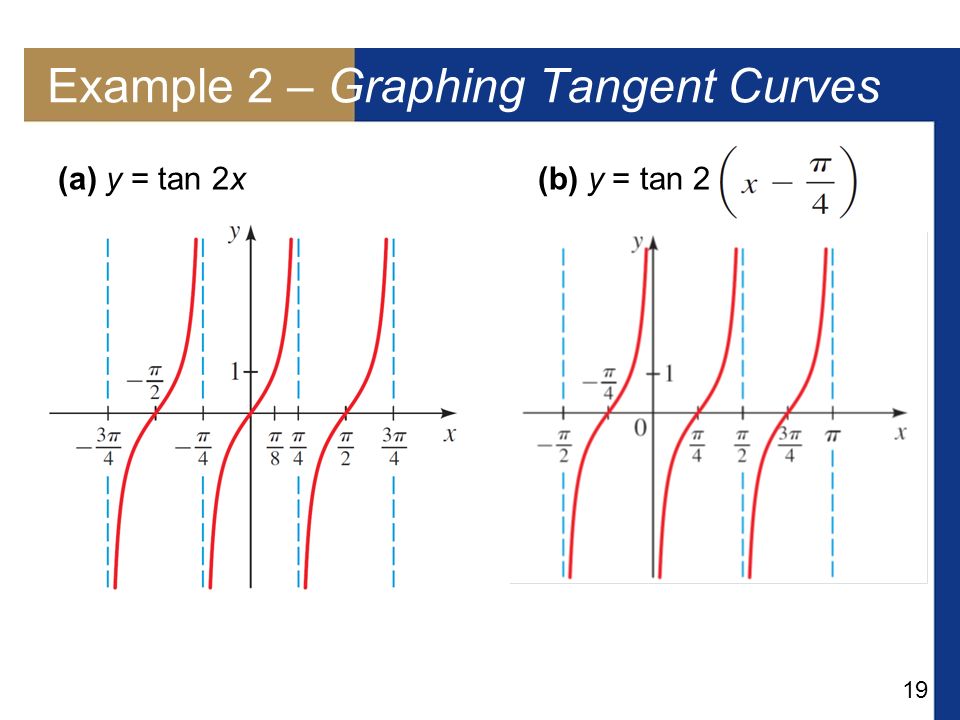


Tan2x ただの悪魔の画像



Answered Find Sin 2x Cos 2x And Tan 2x From Bartleby


Content Graphing The Trigonometric Functions



Howto How To Find Vertical Asymptotes Of Tan2x


Solved Graph Two Periods Of The Given Tangent Function Y Chegg Com
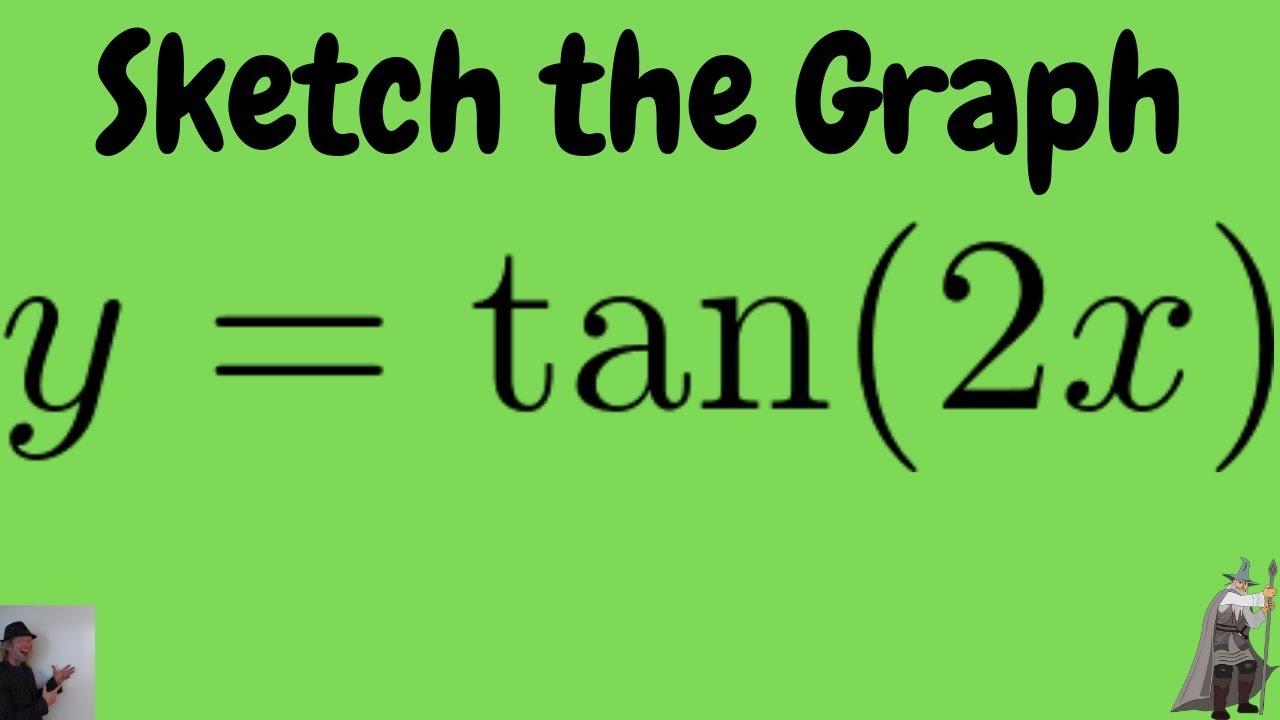


Sketch The Graph Of F X Tan 2x Youtube



Solved Graph Two Periods Of The Given Tangent Function Y Chegg Com


What Is The Graph Of Mod Of Tan X Quora
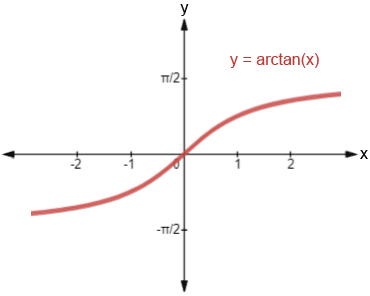


Arctan


Graphs Of The Other Trigonometric Functions Precalculus Ii
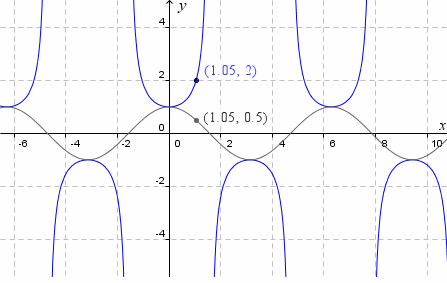


Explore The Slope Of The Tan Curve


13 6 Graphing Trigonometric Functions Graphing Calculator By Mathlab User Manual
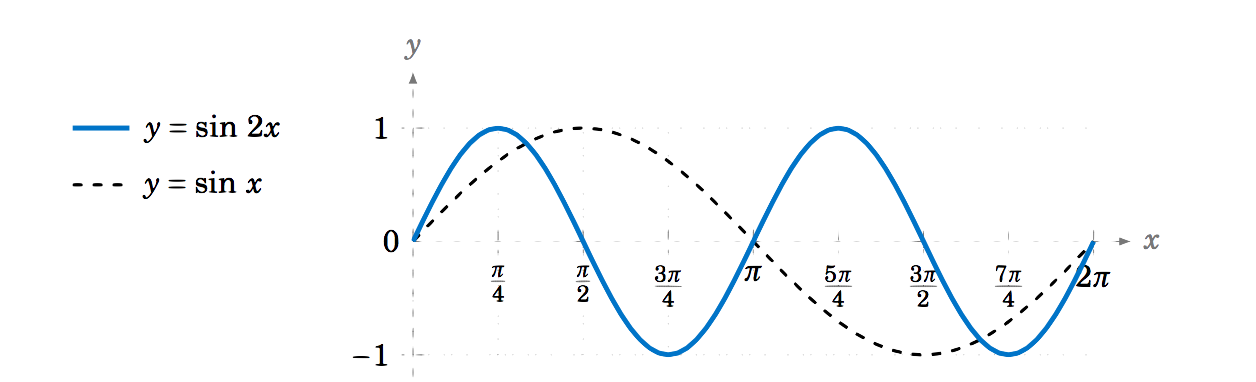


5 2 Properties Of Graphs Of Trigonometric Functions Mathematics Libretexts
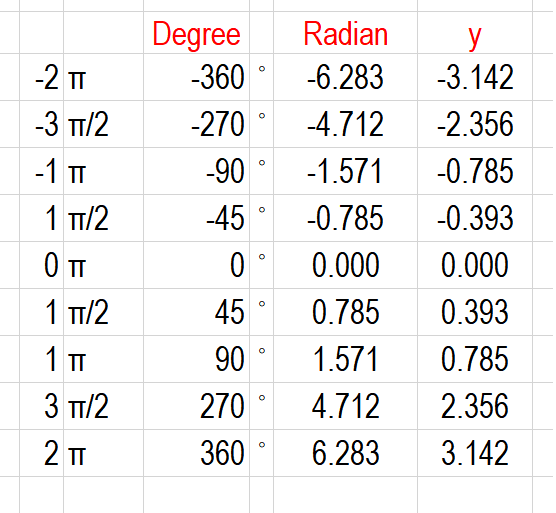


How Do You Graph Y Tan 1 2 X Socratic


Graphing Tangent Functions
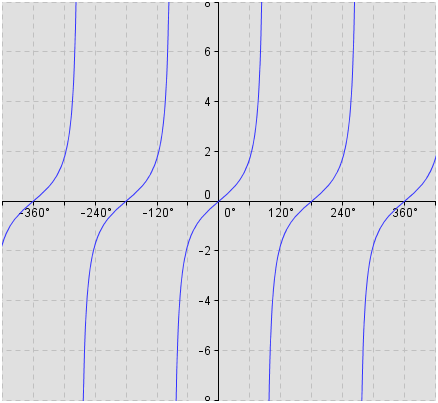


Trigonometry Trigonometric Functions


Content Graphing The Trigonometric Functions


Graphing Trig Functions Geogebra
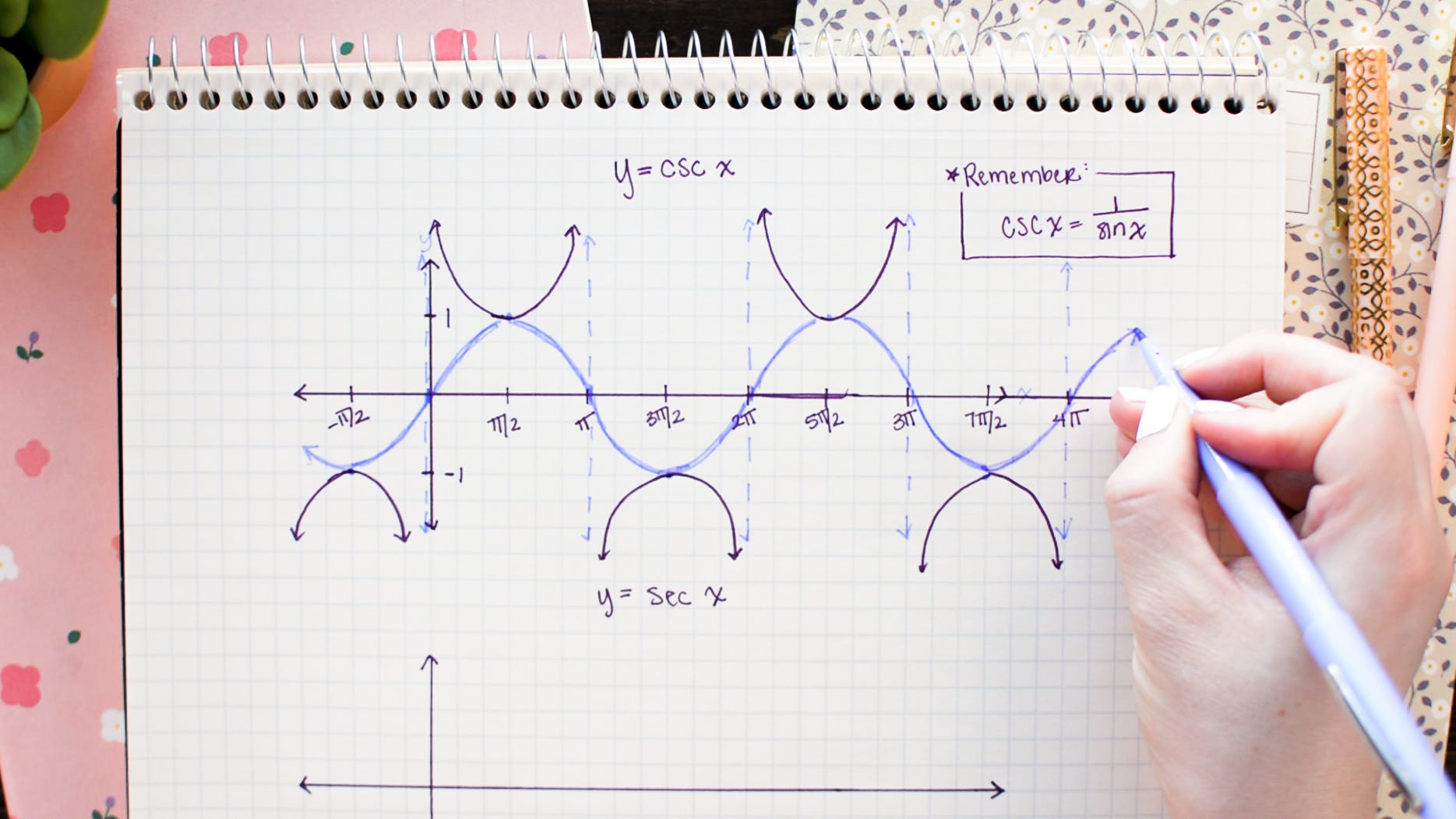


How To Graph Sine Cosine Tangent By Hand By Brett Berry Math Hacks Medium
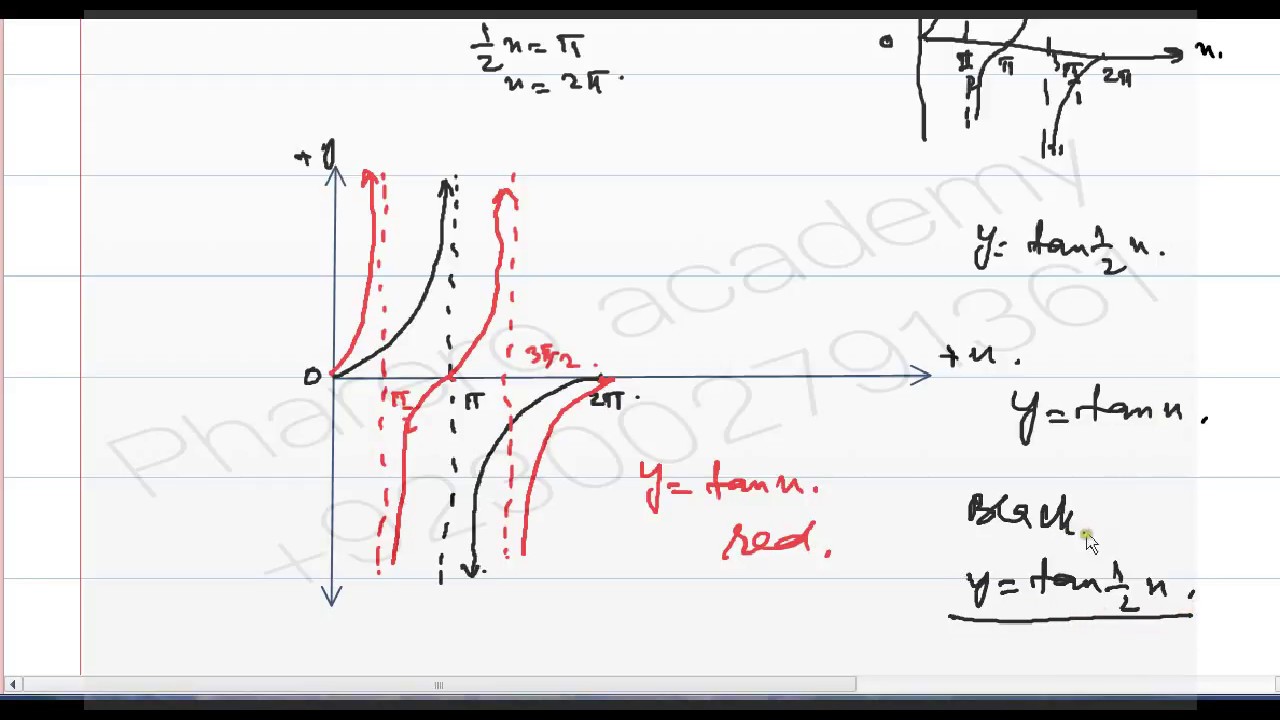


Graph Of Y Tan 1 2 X In Urdu Hindi Youtube



The Tangent Function Functions Siyavula


Warm Upnov 25 Th Determine Whether To Us The Law Of Sine Or Cosine And Solve For The Missing Pieces 1 D Abc With A 12 B 13 C 24 2 D Abc Ppt Download


Bestmaths



6 2 Graphs Of The Other Trigonometric Functions Mathematics Libretexts



Trig Graphs Investigate The Effects Of 2sin X 2cos X 2tan X Ppt Video Online Download


Bestmaths
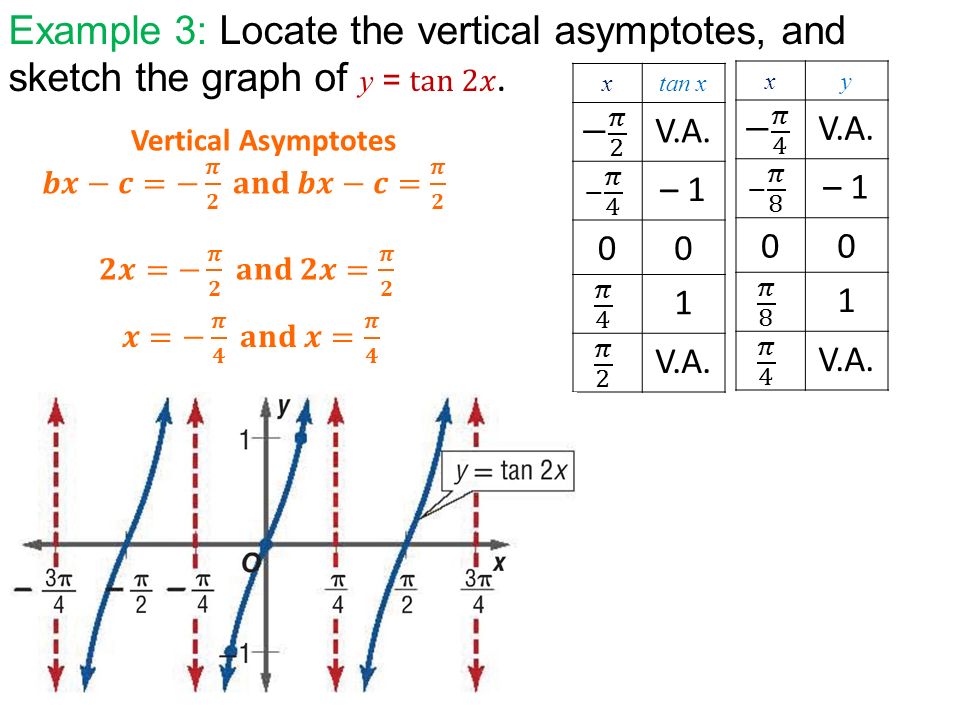


Howto How To Find Vertical Asymptotes Of Tan2x



Trig Transformations Of Graphs



The Equations Y Tan 2 X And Y 1 Are Graphed Below According To The Graphwhich Of The Brainly Com


Graphs Of The Other Trigonometric Functions Precalculus Ii



Trigonometric Functions



The Tangent Function Functions Siyavula


Trigonometry Functions User S Blog


Exact Trig Values



Graph Of Y Tan X Video Trigonometry Khan Academy



How To Graph Tan Ex Y Tan2x Study Com


Solution Y 2 Tan 2x Graph Two Periods Of The Given Tangent Function



Trigonometry Reciprocal Identities Expii
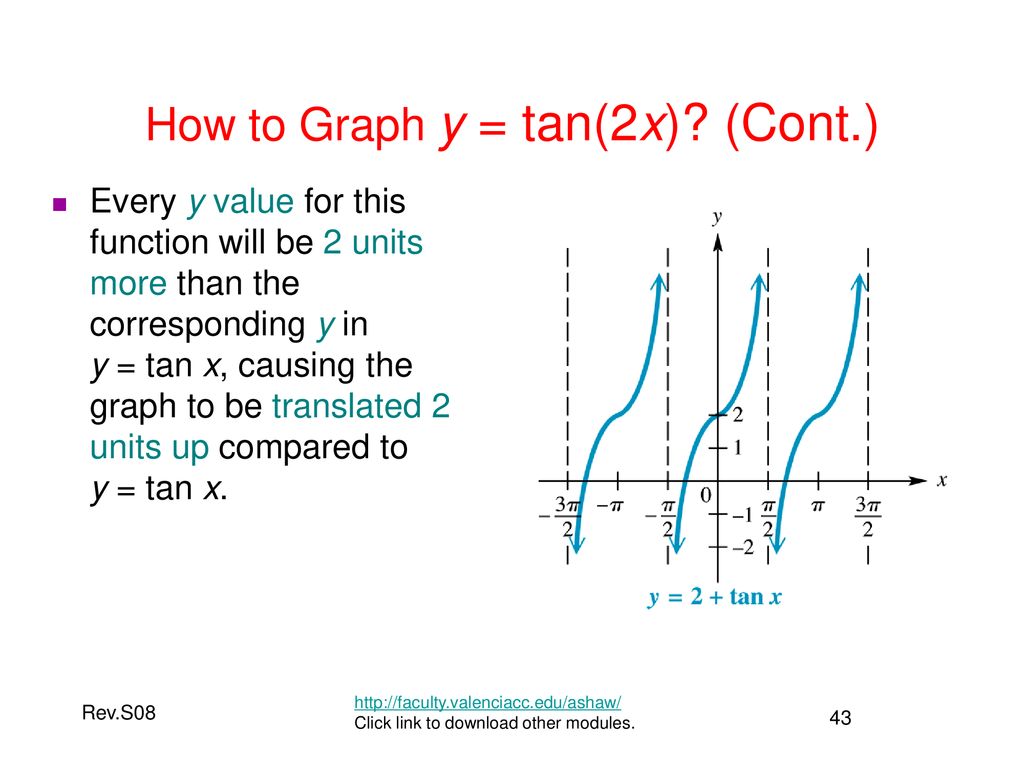


Graphs Of The Circular Functions Ppt Download
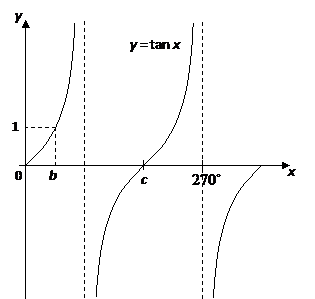


Tangent Graphs Worked Solutions Examples Videos
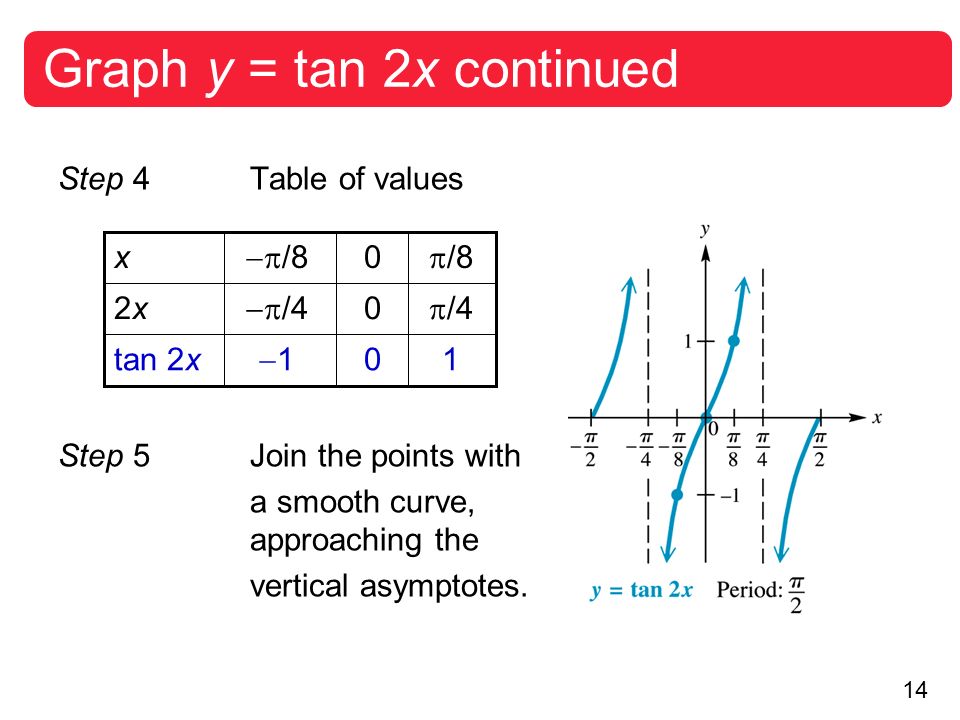


Howto How To Find Vertical Asymptotes Of Tan2x


Trigonometry Functions User S Blog


Period And Phase Shift Intro To Trigonometry


Math Scene Trigonometry Functions Graphs Of Trig Functions Lesson 3



Graphing Tangent Read Trigonometry Ck 12 Foundation


What Is The Graph Of Mod Of Tan X Quora


Howto How To Find Vertical Asymptotes Of Tan2x



Trigonometric Functions


Explore The Slope Of The Tan Curve


Graphs Of The Tangent And Cotangent Functions



0 件のコメント:
コメントを投稿